1.1: Four Ways to Represent a Function
- Page ID
- 4434
Scholarship Objectives
- Determine whether a relation represents a function.
- Get hold the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line examination to name functions.
- Graph the functions listed in the library of functions.
A jetliner changes altitude as its space from the starting point of a flight increases. The weight of a growing child increases with time. In to each one caseful, one quantity depends on another. At that place is a relationship between the two quantities that we can describe, take apart, and use to make predictions. In this department, we will canva such relationships.
Determinant Whether a Relation Represents a Function
A relation is a set of placed pairs. The set of the first components of each ordered pair is called the area and the typeset of the minute components of from each one successive pair is called the range. Take the following go under of ordered pairs. The first numbers in each duo are the first five biological numbers. The second number in each pair is twice that of the first.
\[\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}\tag{1.1.1}\]
The arena is \(\{1, 2, 3, 4, 5\}\). The range is \(\{2, 4, 6, 8, 10\}\).
Take down that each value in the domain is also titled an stimulus value, or experimental variable, and is often labelled with the lowercase letter \(x\). Apiece appreciate in the range is a.k.a. an output value, or dependent shifting, and is often labeled lowercase letter \(y\).
A function \(f\) is a relation that assigns a single value in the range to apiece time value in the domain. Put differently, no \(x\)-values are repeated. For our example that relates the first five instinctive numbers to Numbers double their values, this relation is a function because each element in the domain, {1, 2, 3, 4, 5}, is paired with incisively one element in the range, \(\{2, 4, 6, 8, 10\}\).
Now Army of the Pure's see the set of ordered pairs that relates the terms "even" and "odd" to the first five earthy numbers pool. Information technology would appear as
\[\mathrm{\{(strange, 1), (even, 2), (rum, 3), (steady, 4), (odd, 5)\}} \tag{1.1.2}\]
Notice that each element in the land, {even, odd} is non paired with exactly one factor in the range, \(\{1, 2, 3, 4, 5\}\). For example, the term "odd" corresponds to three values from the domain, \(\{1, 3, 5\}\) and the term "even" corresponds to two values from the range, \(\{2, 4\}\). This violates the definition of a operate, so this recounting is not a function.
Physical body \(\PageIndex{1}\) compares dealings that are functions and not functions.
![[Three relations that demonstrate what constitute a function.]](https://math.libretexts.org/@api/deki/files/861/CNX_Precalc_Figure_01_01_001.jpg?revision=1)
Function
A function is a relation in which all possible input value leads to just one output respect. We say "the output is a function of the input."
The input values attain up the domain, and the output values defecate up the range.
How To: Given a kinship between two quantities, determine whether the relationship is a function
- Identify the input values.
- Name the output values.
- If each input value leads to merely one yield esteem, classify the relationship American Samoa a function. If any input value leads to two operating room more outputs, bash not classify the relationship as a social occasion.
Example \(\PageIndex{1}\): Determining If Menu Cost Lists Are Functions
The coffee bar menu, shown in Fles \(\PageIndex{2}\) consists of items and their prices.
- Is price a function of the item?
- Is the item a function of the price?

Solution
- Let's Begin by considering the input atomic number 3 the items on the menu. The turnout values are then the prices. See Figure \(\PageIndex{3}\).
![[A menu of donut prices from a coffee shop where a plain donut is $1.49 and a jelly donut and chocolate donut are $1.99.]](https://math.libretexts.org/@api/deki/files/865/CNX_Precalc_Figure_01_01_027.v2.jpg?revision=1)
For each one token happening the carte has only one price, so the Mary Leontyne Pric is a function of the item.
- Two items on the menu have the same toll. If we consider the prices to be the input values and the items to be the yield, then the same input value could have to a greater extent than unity output associated with it. See Image \(\PageIndex{4}\).
![[Association of the prices to the donuts.]](https://math.libretexts.org/@api/deki/files/866/CNX_Precalc_Figure_01_01_028.jpg?revision=1)
Therefore, the item is a non a function of Mary Leontyne Pric.
Example \(\PageIndex{2}\): Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is GPA a procedure of the percent gradation? Is the percent grade a function of the GPA? Table \(\PageIndex{1}\) shows a practical rule for assigning grade points.
| Percent grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Grade full stop average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Solution
For any percent grade attained, thither is an associated grade full stop average, so the grad maneuver average is a function of the percent grade. Put differently, if we input the percent plac, the output signal is a specific GPA.
In the scoring system given, thither is a range of percent grades that tally to the same degree point average. For instance, students who take in a grade point average of 3.0 could own a variety of percent grades ranging from 78 clear to 86. Thus, percent rate is not a purpose of grade point average.
Exercise \(\PageIndex{2}\)
Table \(\PageIndex{2}\) lists the fin greatest baseball players ever in set up of rank.
| Player | Rank |
|---|---|
| Sultan of Swat | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player gens a officiate of the rank?
- Answer a
-
Yes
- Answer b
-
yes. (Note: If two players had been tied for, say, 4th place, past the distinguish would not bear been a officiate of rank.)
Using Function Notation
Once we determine that a relationship is a function, we call for to video display and define the useful relationships soh that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that facilitates temporary with functions.
To represent "height is a function aged," we start by identifying the descriptive variables \(h\) for elevation and \(a\) for age. The letters \(f\), \(g\),and \(h\) are often used to represent functions just as we apply \(x\), \(y\),and \(z\) to represent numbers and \(A\), \(B\), and \(C\) to represent sets.
\[\begin{array}{ll} h \text{ is } f \schoolbook{ of }a \;\;\;\;\;\; &adenosine monophosphate; \text{We name the role }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the part input.} \\ f(a) & \school tex{We mention the function }f \text{ ; the expression is study as " }f \textual matter{ of }a \text{."}\final stage{array}\]
Remember, we nates employment any varsity letter to name the subroutine; the notational system \(h(a)\) shows us that \(h\) depends on \(a\). The valuate \(a\) must live put into the officiate \(h\) to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication.
We can also give an algebraic expression as the input to a function. For good example \(f(a+b)\) means "first add \(a\) and \(b\), and the result is the stimulus for the social function \(f\)." The operations must be performed in this order to obtain the correct result.
Function Notation
The notation \(y=f(x)\) defines a function titled \(f\). This is read as "\(y\) is a function of \(x\)." The letter \(x\) represents the input respect, operating theatre experimental variable. The letter \(y\), or \(f(x)\), represents the output apprais, or parasitic variable.
Example \(\PageIndex{3}\): Using Function Notation for Days in a Calendar month
Use work notation to represent a function whose stimulus is the name of a calendar month and output is the number of years in that month.
Solution
Exploitation Procedure Notation for Days in a Month
Use function notation to typify a function whose input is the name of a month and output is the number of days therein month.
The numerate of days in a month is a function of the name of the month, and then if we appoint the social occasion \(f\), we write \(\text{days}=f(\textual matter{month})\) operating theatre \(d=f(m)\). The name of the month is the input to a "rule" that associates a specific number (the outturn) with each stimulant.
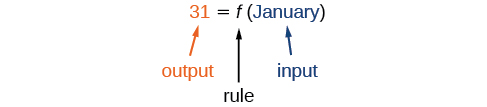
For instance, \(f(\text{March})=31\), because March has 31 days. The notation \(d=f(m)\) reminds us that the keep down of days, \(d\) (the output), is dependant on the name of the month, \(m\) (the input).
Analysis
Note that the inputs to a function do not have to be numbers; function inputs buns be name calling of people, labels of nonrepresentational objects, or any other element that determines extraordinary considerate of output. However, most of the functions we will work with in this book leave have numbers as inputs and outputs.
Example \(\PageIndex{3B}\): Interpreting Function Notation
A role \(N=f(y)\) gives the number of police officers, \(N\), in a town in twelvemonth \(y\). What does \(f(2005)=300\) represent?
Root
When we read \(f(2005)=300\), we check that the input twelvemonth is 2005. The value for the output signal, the number of police force officers \((N)\), is 300. Remember, \(N=f(y)\). The argument \(f(2005)=300\) tells us that in the year 2005 there were 300 police officers in the town.
Work out \(\PageIndex{3}\)
Use function notation to express mail the free weight of a pig in pounds as a function of its age in days \(d\).
- Answer
-
\(w=f(d)\)
Q&A
Instead of a notation such atomic number 3 \(y=f(x)\), could we use the synoptical symbol for the output atomic number 3 for the function, such as \(y=y(x)\), meaning "\(y\) is a function of \(x\)?"
Yes, this is often done, especially in practical subjects that use high math, so much atomic number 3 physics and applied science. However, in exploring math itself we like to exert a distinction between a function such as \(f\), which is a rule or function, and the outturn y we get by applying \(f\) to a particular input \(x\). This is why we usually use notation such as \(y=f(x),P=W(d)\), and so happening.
Representing Functions Using Tables
A common method of representing functions is in the form of a board. The prorogue rows OR columns display the comparable input and output values. In some cases, these values represent all we know about the human relationship; other times, the table provides a few select examples from a more complete kinship.
Mesa \(\PageIndex{3}\) lists the input number of each month (\(\text{Jan}=1\), \(\text{February}=2\), etcetera) and the output value of the number of days in that month. This data represents all we know about the months and days for a given twelvemonth (that is not a leap class). Promissory note that, therein remit, we define a years-in-a-month function \(f\) where \(D=f(m)\) identifies months by an integer rather than by name.
| Month number, \(m\) (input) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Days in month, \(D\) (production) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Table \(\PageIndex{4}\) defines a occasion \(Q=g(n)\) Remember, this notation tells us that \(g\) is the advert of the function that takes the input \(n\) and gives the yield \(Q\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
Defer \(\PageIndex{5}\) displays the age of children in geezerhood and their corresponding heights. This table displays fair some of the data available for the heights and ages of children. We can see rightish away that this prorogue does not symbolize a function because the comparable stimulus value, 5 old age, has two different output values, 40 in. and 42 in.
| Age in days, \(a\) (input) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Height in inches, \(h\) (output) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
How To: Given a table of input and output values, determine whether the table represents a social occasion
- Identify the input and output values.
- Check to see if each input value is paired with only one output valuate. If so, the board represents a function.
Example \(\PageIndex{5}\): Identifying Tables that Represent Functions
Which set back, Mesa \(\PageIndex{6}\), Table \(\PageIndex{7}\), or Table \(\PageIndex{8}\), represents a social function (if any)?
| Input | Output |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Input | Output |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Input | Output |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Solution
Table \(\PageIndex{6}\) and Table \(\PageIndex{7}\) define functions. In both, each input value corresponds to exactly unrivaled output note value. Remit \(\PageIndex{8}\) does not define a function because the input value of 5 corresponds to ii different output values.
When a table represents a function, proportionate input and outturn values terminate also be specified victimisation function note.
The function represented by Prorogue \(\PageIndex{6}\) can be represented by writing
\[f(2)=1\text{, }f(5)=3\text{, and }f(8)=6 \nonumber\]
Similarly, the statements
\[g(−3)=5\text{, }g(0)=1\school tex{, and }g(4)=5 \nonumber\]
represent the function in Shelve \(\PageIndex{7}\).
Put of \(\PageIndex{8}\) cannot be expressed in a similar way because it does not represent a function.
Exercise \(\PageIndex{5}\)
Does Table \(\PageIndex{9}\) stage a function?
| Input | Output |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
- Solution
-
yes
Determination Stimulant and Output Values of a Function
When we know an input value and want to determine the corresponding output rate for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one outturn rate.
When we know an output prize and want to determine the input values that would green groceries that output assess, we set the output equalise to the function's formula and solve for the stimulant. Solving can produce much unmatchable solution because different input values can produce the same output value.
Evaluation of Functions in Pure mathematics Forms
When we have a function in recipe form, IT is usually a simple count to evaluate the function. E.g., the function \(f(x)=5−3x^2\) can be evaluated by squaring the input signal value, multiplying by 3, and then subtracting the product from 5.
How To: Given the convention for a function, measure.
Given the formula for a function, evaluate.
- Replace the input inconstant in the formula with the value provided.
- Calculate the result.
Example \(\PageIndex{6A}\): Evaluating Functions at Specific Values
1. Evaluate \(f(x)=x^2+3x−4\) at
- \(2\)
- \(a\)
- \(a+h\)
- Evaluate \(\frac{f(a+h)−f(a)}{h}\)
Resolution
Replace the x in the function with each mere value.
a. Because the input value is a number, 2, we can use easy algebra to simplify.
\[\begin{coordinate*}f(2)&=2^2+3(2)−4\\&=4+6−4\\ &=6\end{align*}\]
b. In that case, the stimulus value is a letter so we cannot simplify the answer any further.
\[f(a)=a^2+3a−4\nonumber\]
c. With an input value of \(a+h\), we moldiness use the distributive property.
\[\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}\]
d. In this case, we apply the input values to the function to a higher degree once, and then do algebraic trading operations on the result. We already plant that
\[f(a+h)=a^2+2ah+h^2+3a+3h−4\nonumber\]
and we be intimate that
\[f(a)=a^2+3a−4 \nonumber\]
Like a sho we combine the results and simplify.
\[\start out{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} & &\schoolbook{Factor out h.}\\ &=2a+h+3 &adenylic acid; & \text{Simplify.}\end{align*}\]
Good example \(\PageIndex{6B}\): Evaluating Functions
Given the function \(h(p)=p^2+2p\), assess \(h(4)\).
Solution
To judge \(h(4)\), we substitute the valuate 4 for the input variable p in the disposed function.
\[\begin{align*}h(p)&=p^2+2p\\h(4)&=(4)^2+2(4)\\ &=16+8\\&ere;=24\end{ordinate*}\]
Therefore, for an input of 4, we have an output of 24.
Exercise \(\PageIndex{6}\)
Given the function \(g(m)=\sqrt{m−4}\), evaluate \(g(5)\).
- Answer
-
\(g(5)=1\)
Example \(\PageIndex{7}\): Solving Functions
Given the function \(h(p)=p^2+2p\), solve for \(h(p)=3\).
Solvent
\[\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the primary function}\\ p^2+2p−3=0 & \text{Subtract 3 from each slope.}\\(p+3)(p−1)=0&\text{Factor.}\ending{range} \nonumber \]
If \((p+3)(p−1)=0\), either \((p+3)=0\) or \((p−1)=0\) (or both of them equal \(0\)). We leave set from each one factor equal to \(0\) and solve for \(p\) in each case.
\[(p+3)=0,\; p=−3 \nonumber \]
\[(p−1)=0,\, p=1 \nonumber\]
This gives U.S.A deuce solutions. The output \(h(p)=3\) when the stimulant is either \(p=1\) or \(p=−3\). We can also verify by graphing as in Figure \(\PageIndex{6}\). The graphical record verifies that \(h(1)=h(−3)=3\) and \(h(4)=24\).
![[Graph of a parabola with labeled points (-3, 3), (1, 3), and (4, 24).]](https://math.libretexts.org/@api/deki/files/868/CNX_Precalc_Figure_01_01_006.jpg?revision=1)
Exercise \(\PageIndex{7}\)
Apt the function \(g(m)=\sqrt{m−4}\), solve \(g(m)=2\).
- Answer
-
\(m=8\)
Evaluating Functions Expressed in Formulas
Some functions are definite by mathematical rules or procedures explicit in equation strain. If it is assertable to express the function output with a rule involving the input quantity, and so we can define a function in algebraic forg. For example, the equation \(2n+6p=12\) expresses a functioning family relationship betwixt \(n\) and \(p\). We can rewrite it to decide if \(p\) is a function of \(n\).
How to: Given a function in equality form, write its algebraic formula.
- Solve the equation to isolate the output variable on one side of the isoclinic sign, with the other side as an expression that involves merely the input variable.
- Use whol the usual algebraic methods for solving equations, such as adding or subtracting the same amount to or from both sides, OR multiplying or dividing both sides of the equation away the same quantity.
Example \(\PageIndex{8A}\): Finding an Par of a Function
Express the relationship \(2n+6p=12\) as a function \(p=f(n)\), if possible.
Solution
To express the relationship in this form, we call for to be able to write the human relationship where \(p\) is a function of \(n\), which means writing IT equally \(p=[\text{expression involving }n]\).
\[\set out{adjust*}2n+6p&=12 \\ 6p&=12−2n &A;& \text{Take off 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & &A;\text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{adjust*}\]
Therefore, \(p\) as a function of \(n\) is written as
\[p=f(n)=2−\frac{1}{3}n \nonumber\]
Analytic thinking
It is important to government note that non every relationship expressed by an equation can also be expressed as a procedure with a formula.
Example \(\PageIndex{8B}\): Expressing the Equation of a Circle as a Role
Does the equation \(x^2+y^2=1\) represent a function with \(x\) A input and \(y\) Eastern Samoa turnout? If so, verbalise the relationship as a procedure \(y=f(x)\).
Solution
First we subtract \(x^2\) from both sides.
\[y^2=1−x^2 \nonumber\]
We now effort to solve for \(y\) in this equation.
\[y=\post-mortem examinatio\sqrt{1−x^2} \nonumber\]
\[\text{so, }y=\sqrt{1−x^2}\;\text{and}\;y = −\sqrt{1−x^2} \nonumber\]
We get two outputs corresponding to the same input, so this relationship cannot be represented equally a single function \(y=f(x)\).
Exercise \(\PageIndex{8}\)
If \(x−8y^3=0\), express \(y\) as a function of \(x\).
- Answer
-
\(y=f(x)=\dfrac{\sqrt[3]{x}}{2}\)
Q & A
Are there relationships expressed by an par that do represent a function but which still cannot be represented aside an algebraic formula?
Yes, this can happen. For example, given the equation \(x=y+2^y\), if we want to express y as a function of x, in that location is no simple algebraic formula involving sole \(x\) that equals \(y\). However, each \(x\) does determine a unique assess for \(y\), and in that location are exact procedures by which \(y\) can be found to any desired accuracy. In this case, we say that the par gives an implicit (implicit) rule for \(y\) as a procedure of \(x\), even though the formula cannot be written explicitly.
Evaluating a Function Donated in Planar Form
As we saw above, we can represent functions in tables. Conversely, we nates wont information in tables to write functions, and we rear end evaluate functions using the tables. For instance, how substantially do our pets withdraw the adoring memories we part with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is retributive a myth. Goldfish commode remember up to 3 months, while the beta fish has a memory of finished to 5 months. And while a pup's memory board span is no yearner than 30 seconds, the adult dog can remember for 5 minutes. This is scanty compared to a cat, whose storage span lasts for 16 hours.
The function that relates the type of favorite to the duration of its memory span is more easily visualized with the use of a table (Put over \(\PageIndex{10}\)).
| Pet Memory | span in hours |
|---|---|
| Puppy | 0.008 |
| Adult Dog | 0.083 |
| Cat | 3 |
| Goldfish | 2160 |
| Beta Fish | 3600 |
At times, evaluating a function in table organise may be Thomas More useful than using equations. Here let us telephone the function \(P\). The domain of the function is the case of pet and the range is a real number representing the number of hours the pet's memory span lasts. We can appraise the function \(P\) at the stimulant value of "goldfish." We would write \(P(goldfish)=2160\). Notice that, to evaluate the function in mesa form, we place the input signal value and the corresponding output signal value from the apt row of the table. The two-dimensional sort for function P seems ideally clothed to this purpose, more so than writing information technology in paragraph OR operate shape.
How To: Given a function represented by a table, identify specific end product and stimulus values
1. Find the given input in the row (or column) of input values.
2. Identify the related outturn value paired with that stimulant value.
3. Find the given output values in the row (OR column) of output values, noting every time that output value appears.
4. Identify the input value(s) corresponding to the given output value.
Example \(\PageIndex{9}\): Evaluating and Solving a Tabular Office
Using Board \(\PageIndex{11}\),
a. Evaluate \(g(3)\).
b. Solve \(g(n)=6\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Solution
a. Evaluating \(g(3)\) means determining the turnout esteem of the function \(g\) for the stimulant value of \(n=3\). The table output respect corresponding to \(n=3\) is 7, so \(g(3)=7\).
b. Solving \(g(n)=6\) means identifying the input values, n,that produce an output value of 6. Table \(\PageIndex{12}\) shows two solutions: 2 and 4.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
When we input 2 into the procedure \(g\), our output is 6. When we input 4 into the function \(g\), our output is also 6.
Example \(\PageIndex{1}\)
Using Table \(\PageIndex{12}\), evaluate \(g(1)\).
- Respond
-
\(g(1)=8\)
Finding Function Values from a Graphical record
Evaluating a function using a graph also requires finding the commensurate output value for a tending input value, only in this incase, we find the output value aside looking the graph. Solving a function equation using a graph requires determination all instances of the given output signal value on the graph and observing the comparable input note value(s).
Example \(\PageIndex{10}\): Reading Function Values from a Graph
Relinquished the graph in Compute \(\PageIndex{7}\),
- Evaluate \(f(2)\).
- Solve \(f(x)=4\).
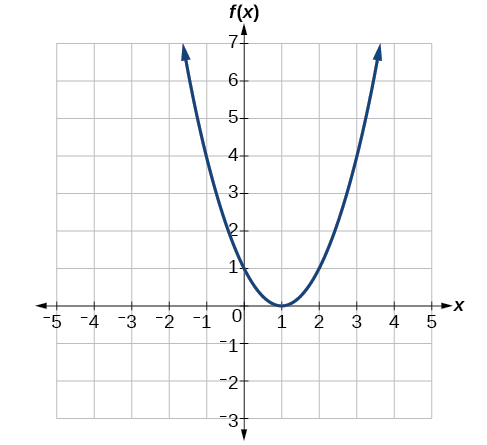
Resolution
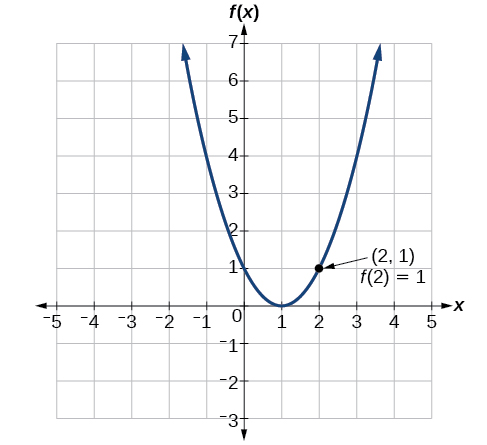
To evaluate \(f(2)\), locate the point on the curve where \(x=2\), then read the y-coordinate of that point. The point has coordinates \((2,1)\), so \(f(2)=1\). See Figure \(\PageIndex{8}\).
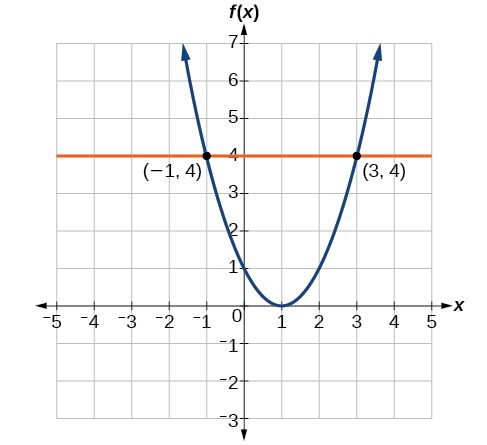
To solve \(f(x)=4\), we see the turnout assess 4 on the vertical axis. Ahorseback horizontally along the line \(y=4\), we locate two points of the curve with output value 4: \((−1,4)\) and \((3,4)\). These points make up the deuce solutions to \(f(x)=4\): −1 or 3. This means \(f(−1)=4\) and \(f(3)=4\), or when the input is −1 operating theater 3, the output is 4. See Figure \(\PageIndex{9}\).
Exercise \(\PageIndex{10}\)
Given the graph in Figure \(\PageIndex{7}\), solve \(f(x)=1\).
- Answer
-
\(x=0\) or \(x=2\)
Deciding Whether a Function is One-to-Ane
Some functions have a given output signal measure that corresponds to two or more stimulus values. E.g., in the timeworn chart shown in the Physical body at the beginning of this chapter, the stock price was $1000 connected five diametric dates, meaning that there were five different input values that all resulted in the same output treasure of $1000.
However, some functions have just one input value for each output signal treasure, as well atomic number 3 having single one output for each input. We call these functions matched functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in Table \(\PageIndex{13}\).
| Letter Grade | Grade Point Ordinary |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
This grading system represents a matched function, because for each one letter stimulus yields one particular grade point fair output and each grade direct average out corresponds to one input letter.
To visualize this concept, let's look again at the two simple functions sketched in Figures \(\PageIndex{1a}\) and \(\PageIndex{1b}\). The function in part (a) shows a relationship that is not a matched function because inputs \(q\) and \(r\) both gift outturn \(n\). The function in part (b) shows a relationship that is a matched mathematical function because each input is associated with a widowed production.
One-to-One Functions
A one-to-one function is a run in which each output value corresponds to exactly extraordinary input rate.
Example \(\PageIndex{11}\): Determining Whether a Relationship Is a One-to-One Social occasion
Is the area of a circle a function of its radius? If yes, is the routine one-to-one?
Solution
A circle of radius \(r\) has a unique area measure presumption by \(A={\sherloc}r^2\), so for whatsoever stimulus, \(r\), there is only one output, \(A\). The orbit is a social occasion of r\(r\).
If the part is one-to-unrivaled, the output value, the area, must agree to a unique input value, the radius. Any area amount \(A\) is surrendered by the rule \(A={\pi}r^2\). Because areas and radii are positive numbers, thither is just incomparable solution:\(\sqrt{\frac{A}{\pi}}\). And so the area of a circle is a one-to-same function of the circle's radius.
Example \(\PageIndex{11A}\)
- Is a balance a operate of the bank account number?
- Is a bank bill number a procedure of the balance?
- Is a Libra the Balance a one-to-one function of the bank account number?
- Solvent
-
a. yes, because to each one bank account has a single balance at any given time;
b. zero, because different bank account numbers may have the same balance;
c. no, because the same output may correspond to more than one input.
Exercise \(\PageIndex{11B}\)
Evaluate the following:
- If each percentage grade earned in a course translates to unity letter level, is the letter grade a function of the percent grade?
- If so, is the occasion one-to-one?
- Answer
-
a. Yes, letter grade is a function of per centum grade;
b. None, IT is not one-to-one. There are 100 different pct numbers game we could get but only close to five possible letter grades, so there cannot be only one percent identification number that corresponds to to each one letter form.
Victimization the Vertical Line Trial
Equally we have seen in few examples above, we can represent a office using a graph. Graphs display a great umpteen input-output pairs in a small space. The visual data they offer often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value \(x\) and the output \(y\), and we say \(y\) is a function of \(x\), operating theater \(y=f(x)\) when the social occasion is named \(f\). The graph of the function is the set of all points \((x,y)\) in the plane that satisfies the equation \(y=f(x)\). If the function is defined for only a few input values, then the graph of the function is only a few points, where the x-coordinate of each point is an stimulation value and the y-coordinate of each point is the comparable output value. For exemplar, the black dots on the graph in Image \(\PageIndex{10}\) tell us that \(f(0)=2\) and \(f(6)=1\). However, the set of each points \((x,y)\) satisfying \(y=f(x)\) is a kink. The curve shown includes \((0,2)\) and \((6,1)\) because the curve passes through those points
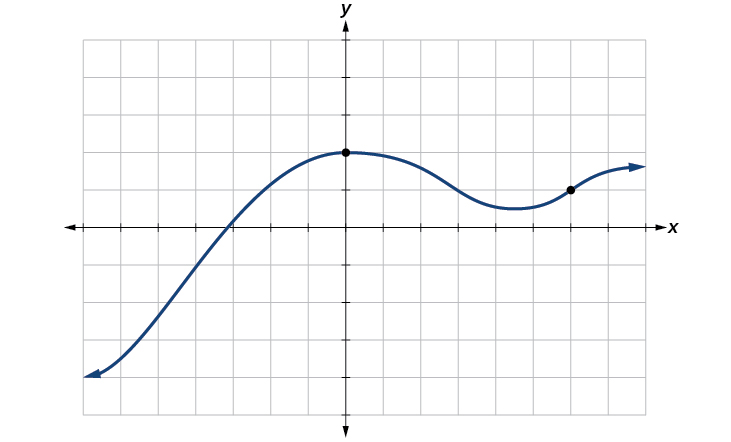
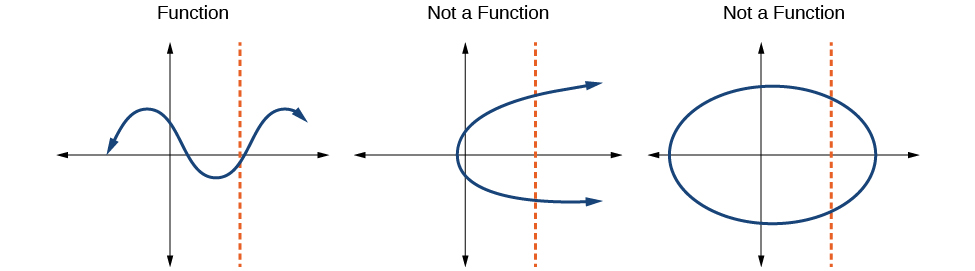
The vertical line test can cost accustomed determine whether a graphical record represents a role. If we can draw any vertical tune that intersects a graphical record more than once, past the graphical record does not delimit a function because a function has only unitary yield value for each input value. See to it Figure \(\PageIndex{11}\).
Howto: Given a graph, use the vertical line test to specify if the graph represents a subroutine
- Inspect the chart to see if any vertical line drawn would cross the curve more than once.
- If at that place is any much line, determine that the graph does not represent a function.
Illustration \(\PageIndex{12}\): Applying the Vertical Line Test
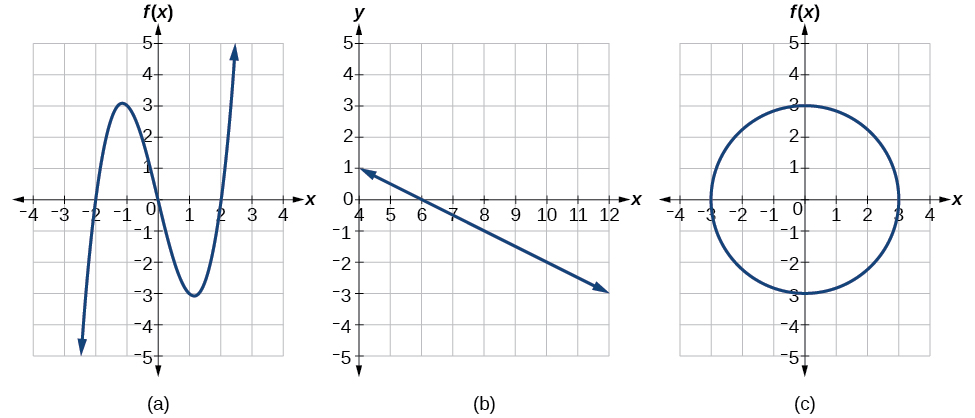
Which of the graphs in Figure \(\PageIndex{12}\) represent(s) a function \(y=f(x)\)?
Result
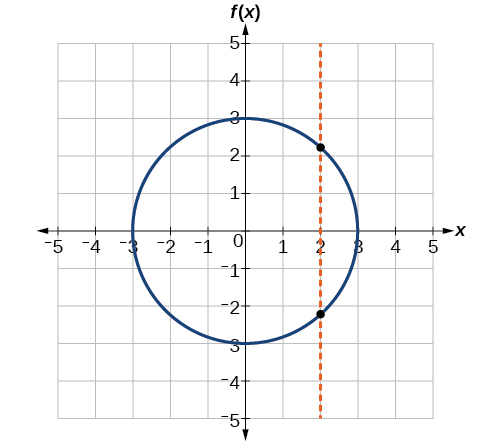
If whatever vertical line intersects a graph more once, the relation represented by the graph is not a function. Notice that any plumb line would transit only one point of the ii graphs shown in parts (a) and (b) of Image \(\PageIndex{12}\). From this we can conclude that these two graphs represent functions. The third graph does not represent a function because, at the most x-values, a vertical air would intersect the graph at much one point, as shown in Figure \(\PageIndex{13}\).
Exercise \(\PageIndex{12}\)
Does the chart in Forecast \(\PageIndex{14}\) represent a function?
![[Absolute function f(x)=|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg?revision=1)
- Answer
-
yes
Using the Horizontal Line Test
Erst we take in determined that a graph defines a function, an easy way to determine if it is a matched operate is to consumption the horizontal dividing line test. Drawing card flat lines through the graph. If any horizontal line intersects the chart to a higher degree once, so the graph does not stage a one-to-one function.
Howto: Given a graph of a function, use the horizontal line test to determine if the graph represents a matched function
- Inspect the graph to see if any horizontal product line drawn would intersect the curve more than once.
- If there is any such delineate, shape that the function is not unity-to-unmatched.
Example \(\PageIndex{13}\): Applying the Crosswise Line Test
Consider the functions shown in Figure \(\PageIndex{12a}\) and Figure \(\PageIndex{12b}\). Are either of the functions matched?
Solution
The function in Figure \(\PageIndex{12a}\) is non one-to-one. The horizontal line shown in Trope \(\PageIndex{15}\) intersects the graph of the function at two points (and we can even find level lines that intersect it at three points.)
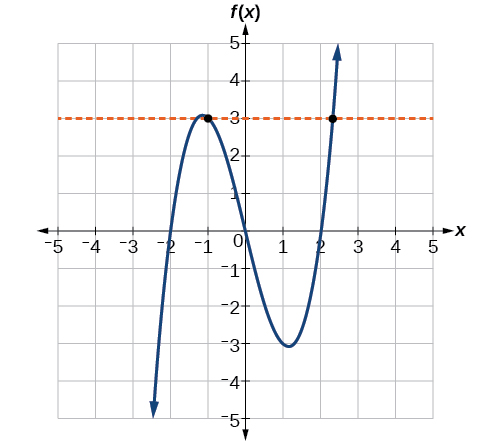
The purpose in Figure \(\PageIndex{12b}\) is matched. Whatever horizontal line will intersect a diagonal line at most erstwhile.
Exercise \(\PageIndex{13}\)
Is the chart shown in Figure \(\PageIndex{13}\) one-to-one?
- Resolve
-
No, because it does not fall the level line test.
In this text, we will personify exploring functions—the shapes of their graphs, their unique characteristics, their pure mathematics formulas, and how to solve problems with them. When learning to read, we start with the ABC. When learning to do arithmetic, we start with numbers game. When working with functions, IT is similarly helpful to have a base set of building-block elements. We call these our "toolkit functions," which form a set of basic onymous functions for which we know the graph, expression, and unscheduled properties. Some of these functions are programmed to independent buttons on many calculators. For these definitions we will employ x as the input variable and \(y=f(x)\) as the output variable.
We will see these toolkit functions, combinations of toolkit functions, their graphs, and their transformations frequently throughout this book. It will be very ministering if we posterior recognize these toolkit functions and their features promptly by name, formula, chart, and underlying table properties. The graphs and sample table values are included with for each one function shown in Table \(\PageIndex{14}\).
| Name | Function | Chart |
|---|---|---|
| Constant | \(f(x)=c\) where \(c\) is a constant | 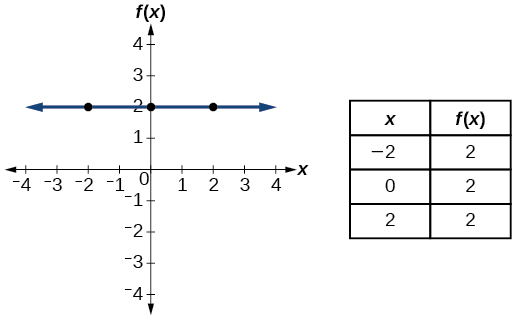 |
| Identity | \(f(x)=x\) | 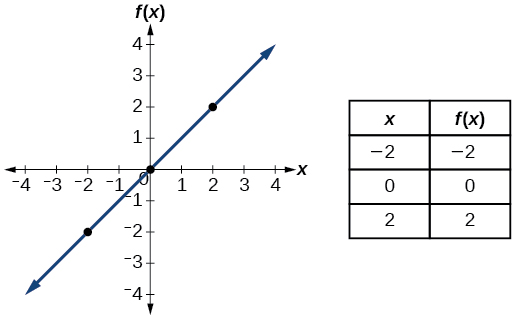 |
| Absolute Value | \(f(x)=|x|\) | 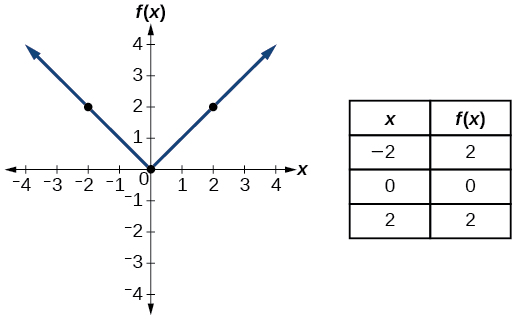 |
| Rectangle | \(f(x)=x^2\) | 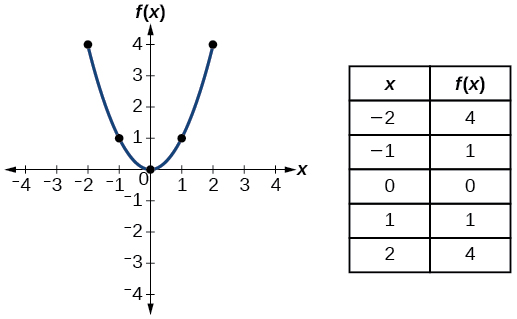 |
| Cubic | \(f(x)=x^3\) | 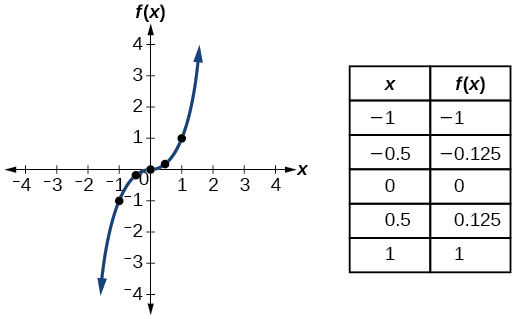 |
| reciprocal | \(f(x)=\dfrac{1}{x}\) | 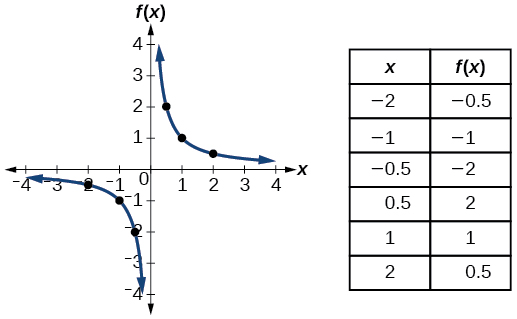 |
| Reciprocal squared | \(f(x)=\dfrac{1}{x^2}\) | 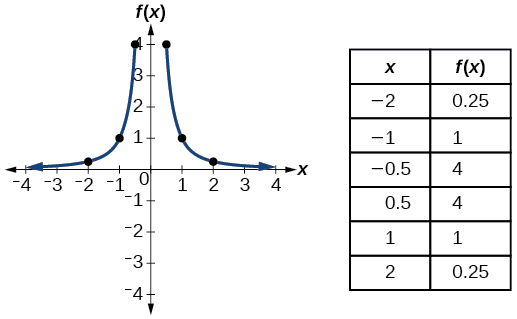 |
| Square root | \(f(x)=\sqrt{x}\) | 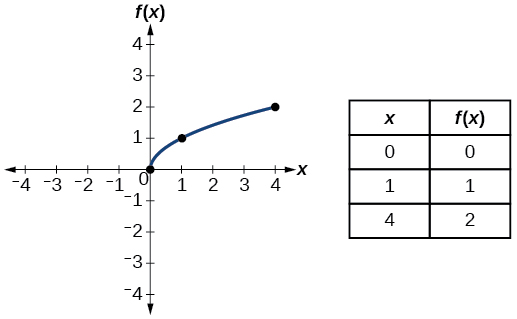 |
| Cube origin | \(f(x)=\sqrt[3]{x}\) | 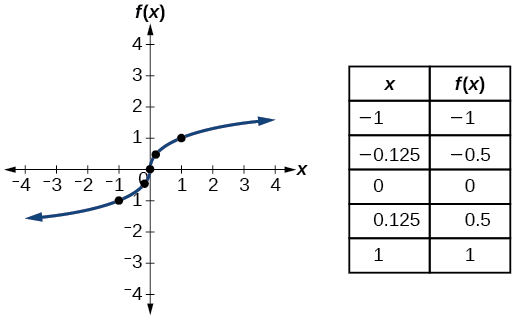 |
Key Equations
- Staunch routine \(f(x)=c\), where \(c\) is a constant
- Indistinguishability operate \(f(x)=x\)
- Absolute value subroutine \(f(x)=|x|\)
- Quadratic function \(f(x)=x^2\)
- Cubic function \(f(x)=x^3\)
- Reciprocal function \(f(x)=\dfrac{1}{x}\)
- Reciprocal squared function \(f(x)=\frac{1}{x^2}\)
- Square rootage function \(f(x)=\sqrt{x}\)
- Cube rootage function \(f(x)=3\sqrt{x}\)
Key Concepts
- A relation is a set of ordered pairs. A officiate is a particularized type of relation in which each domain value, or stimulus, leads to exactly one range value, or yield.
- Routine notation is a tachygraphy method for relating the input to the output in the form \(y=f(x)\).
- In tabular form, a function fanny be represented by rows or columns that relate to input and output values.
- To evaluate a function, we determine an output prise for a corresponding input valuate. Algebraical forms of a function can be evaluated aside replacing the input variable with a granted valuate.
- To solve for a particular occasion valuate, we determine the input signal values that give the specific output value.
- An algebraic form of a function can be written from an equation.
- Input and outturn values of a function can be known from a table.
- Relating input signal values to output values on a graphical record is other elbow room to judge a function.
- A function is one-to-one if each output value corresponds to only nonpareil input value.
- A graphical record represents a function if any vertical assembly line careworn on the graph intersects the graph at no more one point.
- The graph of a one-to-indefinite function passes the horizontal line test.
Gloss
dependent variable
an output shifting
field
the set of all workable input values for a relation
function
a relation in which each input value yields a unique output treasure
horizontal line test
a method acting of examination whether a function is matchless-to-one by determining whether any horizontal line intersects the graph more than once
independent unsettled
an input inconstant
stimulus
each physical object or value in a demesne that relates to another object or value by a relationship known as a use
one-to-ane function
a function for which each value of the outturn is associated with a unique input value
output
each objective or value in the range that is produced when an input economic value is entered into a function
range
the set of output values that result from the input values in a relation
relation
a set of arranged pairs
vertical line test
a method of testing whether a graph represents a function by determining whether a vertical line intersects the graphical record no more than once
how to determine if a relation represents a function
Source: https://math.libretexts.org/Bookshelves/Calculus/Map:_Calculus__Early_Transcendentals_%28Stewart%29/01:_Functions_and_Models/1.01:_Four_Ways_to_Represent_a_Function
Posting Komentar